Задание 1. Из 6 + (К +
М)(mod6) сотрудников отдела коммерческого банка, среди которых трое мужчин, а
остальные женщины, случайным образом
формируется комиссия из трех
человек. Найти вероятность того, что в комиссии:
а) будет только одна женщина;
b) будут две женщины;
с) будет не менее двух женщин;
d) будет хотя бы одна женщина;
е) будут лица одного пола.
Здание 2. В партии
из 100 + ((К + М)(mod6)) металлических конструкций 40 + ((К +М)(mod6))
изготовлены на первом заводе, 30 + ((К + М)(mod6)) – на втором,
а остальные – на третьем.
Известно, что первый завод производит в среднем (90 + ((К + М)(mod6))%
стандартной продукции, второй – (80 + ((К + М)(mod6))%,
третий – (85 + ((К + М)(mod6))%.
Для контроля качества из всех имеющихся металлических конструкций наугад берут
два.
1. Определить вероятность того,
что по крайней мере одна из проверяемых конструкций будет иметь брак.
2. Обе проверяемые конструкции
оказались стандартными. На каких заводах
вероятнее всего они изготовлены?
Задание 3. По
статистическим данным в городе N в среднем (85 + ((К + М)(mod6))%
новорожденных доживают до 50 лет.
1. Какова вероятность того, что
из 5 + (К + М)(mod4) новорожденных в одном из роддомов города N до 50 лет не
доживет:
а) ровно 3 + (К + М)(mod4); b)
более 3+(К+М)(mod4);
с) менее 3 + (К + М)(mod4); d)
хотя бы один ребенок?
2. Вычислить вероятность того,
что из ста новорожденных города N до 50 лет доживет:
а) 82 + (К + М)(mod6); b) не
менее 82 + (К + М)(mod6);
с) не более 88 + (К + М)(mod6);
d) не менее 80 + (К + М)(mod6), но не более
90 + (К + М)(mod6) детей.
Задание 4. Студент
знает 20 + (К + М)(mod6) вопросов из имеющихся 30 + (К + М)(mod6) вопросов
программы некоторой учебной дисциплины.
На экзамене ему предлагается три
наугад выбранных вопроса из программы. Рассматривается случайная величина
(с.в.) ξ – количество известных студенту вопросов среди заданных.
Составить ряд распределения с.в. ξ
и представить его графически.
Найти функцию распределения с.в. ξё
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Определить вероятности: а) Р{ξ<Mξ}; b) Р{ξ>Mξ+1};
c) Р{|ξ-Mξ|≤σ(ξ)}
Задание 5. Время
ξ (в тыс. часах) до выхода из строя авиационного двигателя, выработавшего
гарантийный ресурс в 2 + (К + М)(mod6) тыс. часов,
является случайным с плотностью
распределения
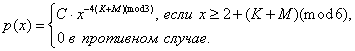
Установить неизвестную
постоянную С и построить график функции p(x).
Найти функцию распределения с.в. ξ
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Во сколько раз число выходов из
строя авиационных двигателей со временем работы после гарантийного срока меньше
среднего превышает число выходов
из строя авиационных двигателей
со временем работы после гарантийного срока больше среднего?
Задание 6. При помощи дальномера произведено 25 измерений
расстояния до некоторого объекта. Получены следующие результаты (в км.)*
9.863, 10.060, 9.985,
10.170, 10.050, 10.130, 10.440, 10.410, 10.180, 9.890,
10.380, 9.709, 10.200, 9.977,
10.090, 10.130, 10.200, 10.320, 10.480, 10.130, 10.130, 10.030, 10.140,
10.190, 10.220
Необходимо:
1. Определить исследуемый признак
и его тип (дискретный или непрерывный).
2. В зависимости от типа признака
построить полигон или гистограмму относительных частот.
3. На основе визуального анализа полигона
(гистограммы) сформулировать гипотезу о законе распределения признака.
4. Вычислить выборочные
характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое
(стандартное) отклонение.
5. Используя критерий согласия
«хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в
п.3 закону распределения при уровне значимости 0,01.
6. Для генеральной средней и
дисперсии построить доверительные интервалы, соответствующие доверительной
вероятности 0,99.
7. С надежностью 0,99 проверить
гипотезу о равенстве:
а) генеральной средней значению
8×С;
б) генеральной дисперсии значению
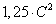 , где C
= 1 + (K + M)/100.
, где C
= 1 + (K + M)/100.
* Для получения Ваших конкретных
данных все значения выборки следует умножить на число
C = 1 + (K + M)/100.



