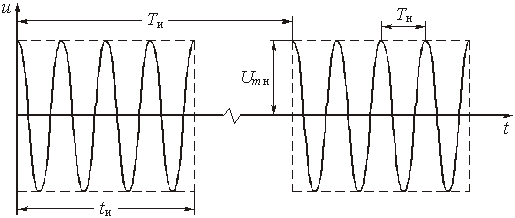
На входе полосового фильтра действуют
периодические прямоугольные радиоимпульсы (рис. 1.1) с параметрами: tи
– длительность импульсов, Tи – период следования; Tн –
период несущей частоты; Umн – амплитуда несущего колебания, имеющего
форму гармонического uн(t) = Umн × cos wнt.
Требуется рассчитать двусторонне
нагруженный пассивный полосовой LC-фильтр и активный полосовой RC-фильтр для
выделения эффективной части спектра радиоимпульсов, лежащей в полосе частот от
(fн – 1/tи) до (fн + 1/tи) (главный
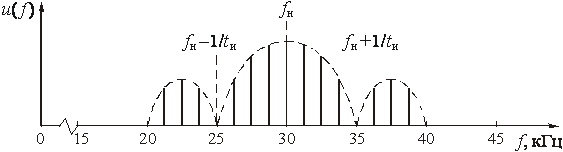
«лепесток спектра»). График модуля спектральной функции U(f) = |U(jf)|
радиоимпульса приведен на рис. 1.2. Спектр имеет дискретный характер, поэтому
частоты fп1 и fп2 границы полосы пропускания фильтров
определяются крайними частотами в главном «лепестке спектра».
Рисунок
1.1
Рисунок
1.2
Частоты fз1 и fз2
полосы задерживания (непропускания) фильтра определяются частотами первых
дискретных составляющих, лежащими слева от (fн – 1/tи) и
справа от (fн + 1/tи). Конкретное определение численных значений
всех частот показано в типовом примере расчета LC-фильтра.
Исходные данные для расчета приведены
в таблицах 1.1 и 1.2. Сопротивления генератора радиоимпульсов Rг и
сопротивление нагрузки Rн пассивного фильтра одинаковы: Rг
= Rн = R. Для вариантов 01¸25 и 51¸75 R = 600 Ом, для вариантов 26¸50 и 76¸99 R = 1000
Ом. Характеристика фильтра аппроксимируется полиномом Чебышева.
Данные таблицы 1.1
|
Тн, мкс
|
tи, мкс
|
Ти, мкс
|
DА, дБ
|
Апол, дБ
|
|
10
|
40
|
115
|
3
|
35
|
Данные таблицы 1.2
Umн, = 11 В
В ходе выполнения курсовой работы
необходимо:
1.
Рассчитать и построить график
амплитудного спектра радиоимпульсов.
2.
Определить частоты fп2 и fз2 и
рассчитать превышение амплитуды частоты fп2 над амплитудой частоты fз2 в децибелах в виде соотношения А' = 20lgUmп/Umз на входе фильтра.
3.
Рассчитать минимально допустимое
ослабление фильтра в полосе задерживания Аmin = Апол
– A'.
4.
Рассчитать порядок m
НЧ-прототипа требуемого фильтра.
5.
Получить выражение для
передаточной функции НЧ-прототипа при аппроксимации его характеристики полиномом
Чебышева.
6.
Осуществить реализацию
двухсторонне нагруженного полосового LC-фильтра.
7.
Осуществить реализацию полосового ARC-фильтра.
8.
Привести ожидаемую характеристику
ослабления полосового фильтра в зависимости от частоты, т. е. A = K(f).
9.
Рассчитать ослабление ARC-фильтра
на границах полосы пропускания и полосы непропускания (задерживания).
10.
Привести схему ARC-полосового
фильтра.



