Задача 1.
Вычислить двойной интеграл 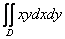 , если область D образует треугольник с вершинами А ( 0; 7), В ( 1; -4), С ( -3;
-2).
, если область D образует треугольник с вершинами А ( 0; 7), В ( 1; -4), С ( -3;
-2).
Задача 2.
Закон распределения системы двух дискретных
случайных величин (X, У) задан следующей таблицей
|
Х \
У
|
-4
|
-3
|
-2
|
1
|
|
-1
|
0
|
0,1
|
0,05
|
0,1
|
|
1
|
0,1
|
0,05
|
0,05
|
0,05
|
|
2
|
0,2
|
0,05
|
0
|
0,1
|
|
4
|
0,05
|
0
|
0,1
|
0
|
Найти а) законы
распределения случайных величин X и У; б) условный
закон распределения случайной величины X при условии, что У = 1; в) математические ожидания М(X), М(У) и центр рассеивания; г) дисперсии D(X) и D(Y); д)
корреляционный момент Сxy и коэффициент
корреляции rxy.
Задача 3.
В результате испытания случайная величина X приняла следующие значения:
Х1
= 6, Х2 = 5, Х3 = 3, Х4 = 2,
Х5
= 3, Х6 = 4, Х7 = 1, Х8 = 2,
X9 = 3, Х10 = 6, Х11 = 4, X12 = 4,
Х13
= 9, Х14 = 3, Х15 = 3, Х16 = 6.
Требуется: а)
построить статистическое распределение; б) изобразить полигон распределения; в)
построить эмпирическую функцию распределения; г) считая величину X непрерывной, составить таблицу
статистического распределения, разбив промежуток ( 0; 10) на пять участков,
имеющих одинаковые длины; построить гистограмму относительных частот.
Задача 4.
Даны 15 выборочных значений Х1,Х2...,
Х15
|
-1,399
|
-1,189
|
-2,069
|
-1,998
|
-0,956
|
|
-1,994
|
-0,864
|
-1,885
|
-1,361
|
-1,304
|
|
-2,008
|
-1,393
|
-1,047
|
-1,927
|
-1,329
|
случайной
величины X, имеющей нормальный закон распределения с
неизвестными параметрами а и 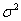 . Требуется: а) вычислить точечные оценки а*,
. Требуется: а) вычислить точечные оценки а*,
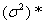 параметров а и
параметров а и
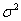 , принимая
, принимая 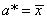 ,
,
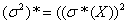 ; записать
функцию плотности и найти Р(Х > -1,5); б) построить доверительные интервалы
для параметров а и σ с надежностью 0,99; в) используя χ2-критерий
и критерий согласия Колмогорова-Смирнова с уровнем значимости ε = 0,1,
оценить согласованность эмпирического и теоретического законов распределения,
разбив интервал
; записать
функцию плотности и найти Р(Х > -1,5); б) построить доверительные интервалы
для параметров а и σ с надежностью 0,99; в) используя χ2-критерий
и критерий согласия Колмогорова-Смирнова с уровнем значимости ε = 0,1,
оценить согласованность эмпирического и теоретического законов распределения,
разбив интервал 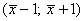 на
5 равных частей.
на
5 равных частей.
Задача 5.
По данным корреляционной таблицы
|
X \ Y
|
10
|
20
|
30
|
40
|
50
|
nx
|
|
5
|
2
|
|
|
|
|
2
|
|
10
|
6
|
7
|
|
|
|
13
|
|
15
|
|
3
|
2
|
1
|
|
6
|
|
20
|
|
|
40
|
10
|
4
|
54
|
|
25
|
|
|
2
|
13
|
7
|
22
|
|
30
|
|
|
|
|
3
|
3
|
|
ny
|
8
|
10
|
44
|
24
|
14
|
n = 100
|
а) найти
условные средние 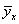 и
и
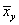 ; б) оценить
тесноту линейной связи между случайными величинами X и Y, а также обоснованность связи
между этими величинами; в) составить уравнения линейной регрессии Y по X и X по У; г)
сделать чертеж, нанеся на него условные средние и прямые регрессии.
; б) оценить
тесноту линейной связи между случайными величинами X и Y, а также обоснованность связи
между этими величинами; в) составить уравнения линейной регрессии Y по X и X по У; г)
сделать чертеж, нанеся на него условные средние и прямые регрессии.



