Задание 3
Для сигнализации на складе
установлены три независимо работающих устройства. Вероятность того, что при
необходимости первое устройство сработает, составляет Р1,
для второго и третьего устройства
эти вероятности равны соответственно Р2 и Р3. Найти вероятность
того, что в случае необходимости сработают:
а) все устройства;
б) только одно устройство;
в) хотя бы одно устройство.
р1 = 95%; р2
= 90%; р3 = 75%;
Задание 18
В партии, состоящей из n одинаково
упакованных изделий, смешаны изделия двух сортов, причем k из этих изделий –
первого сорта, а остальные изделия – второго сорта.
Найти вероятность того, что взятые
наугад два изделия окажутся:
а) одного сорта;
б) разных сортов.
n = 55; k =
35;
Задание 28
Страховая компания разделяет
застрахованных по классам риска: I класс – малый риск, II класс – средний риск,
III класс – большой риск. Среди клиентов компании 50 % – клиенты
первого класса риска, 30% – второго
и 20% – третьего. Вероятность необходимости выплачивать страховое
вознаграждение для первого класса риска равна 0,01, второго 0,03, третьего
0,08.
а) Какова вероятность того, что
застрахованный получит денежное вознаграждение за период страхования?
б) Найти вероятность того, что
получивший денежное вознаграждение застрахованный относится к группе малого
риска.
Задание 33
Вероятность того, что в результате
проверки изделию будет присвоен знак «изделие высшего качества» равна p.
1) На контроль поступило n изделий.
Какова вероятность того, что знак высшего качества будет присвоен:
а) ровно m изделиям;
б) более чем k изделиям;
в) хотя бы одному изделию;
г) указать наивероятнейшее
количество изделий, получивших знак высшего качества, и найти соответствующую
ему вероятность.
2). При тех же условиях найти
вероятность того, что в партии из N изделий знак высшего качества
получает:
а) ровно половина изделий;
б) не менее чем k1, но
не более, чем k2 изделий.
n=6; p=0,2; m=3; k=4;
N=28; k1= 4; k2=14.
Задание 50
В лотерее на каждые 100 билетов
приходится m1 билетов с выигрышем a1 тыс. рублей, m2
билетов с выигрышем a2 тыс. рублей, m3 билетов с
выигрышем a3 тыс. рублей и т.д.
Остальные билеты из сотни не
выигрывают.
Составить закон распределения
величины выигрыша для владельца одного билета и найти его основные
характеристики: математическое ожидание, дисперсию и среднее
квадратическое отклонение. Пояснить
смысл указанных характеристик.
а1=5;
а2=4; а3= 3; а4=
2;
m1=8; m2=10;
m3=15; m4=25.
Задание 58
Вес изготовленного серебряного
изделия должен составлять а граммов.
При изготовлении возможны случайные
погрешности, в результате которых вес изделия случаен, но подчинен нормальному
закону распределения со средним
квадратическим отклонением σ
граммов.
Требуется найти вероятность того,
что:
а) вес изделия составит от α
до β граммов;
б) величина погрешности в весе не
превзойдет δ граммов по абсолютной величине.
a = 130; σ = 5; α = 125; β
= 140; δ = 12;
Задание 70
По итогам выборочных обследований
для некоторой категории сотрудников величина их дневного заработка X руб. и
соответствующее количество сотрудников ni
представлены в виде интервального
статистического распределения.
а) Построить
гистограмму относительных частот распределения.
б) Найти основные характеристики
распределения выборочных данных: среднее выборочное значение, выборочную
дисперсию и выборочное среднее квадратическое отклонение.
в) Оценить генеральные
характеристики по найденным выборочным характеристикам.
г) Считая, что значения признака X
в генеральной совокупности подчинены нормальному закону распределения, найти
доверительный интервал для оценки математического
ожидания (генерального среднего
значения) с надежностью γ , считая, что генеральная дисперсия равна
исправленной выборочной дисперсии.
|
X
|
80-82
|
82-84
|
84-86
|
86-88
|
88-90
|
|
|
ni
|
3
|
7
|
20
|
15
|
5
|
g = 0,88
|
Задание 73
С целью анализа взаимного влияния
прибыли предприятия и его издержек выборочно были проведены наблюдения за этими
показателями в течение ряда месяцев:
X – величина месячной прибыли в
тыс. руб., Y – месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и
представлены в виде корреляционной таблицы, где указаны значения признаков X и
Y и количество месяцев, за которые наблюдались
соответствующие пары значений названных
признаков.
а) По данным корреляционной таблицы
найти условные средние 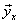 и
и 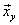 .
.
б) Оценить тесноту линейной связи
между признаками X и Y.
в) Составить уравнения линейной
регрессии Y по X и X по Y .
г) Сделать чертеж, нанеся на него
условные средние и найденные прямые регрессии.
д) Оценить силу связи между
признаками с помощью корреляционного отношения.
|
X
Y
|
30
|
40
|
50
|
60
|
70
|
ny
|
|
5
|
1
|
|
|
|
|
|
|
10
|
5
|
5
|
|
|
|
|
|
15
|
|
3
|
2
|
4
|
|
|
|
20
|
|
|
4
|
1
|
4
|
|
|
25
|
|
|
2
|
7
|
6
|
|
|
30
|
|
|
|
|
3
|
|
|
nx
|
|
|
|
|
|
|



