Задание 1

Для сигнализации на складе установлены три независимо работающих устройства. Вероятность того, что при необходимости первое устройство сработает, составляет Р₁, для второго

и третьего устройства эти вероятности равны соответственно Р₂ и Р₃. Найти вероятность того, что в случае необходимости сработают:

а) все устройства;

б) только одно устройство;

в) хотя бы одно устройство.

р₁ = 70%;        р₂ = 85%;        р₃ = 90%;

Задание 20

В партии, состоящей из n одинаково упакованных изделий, смешаны изделия двух сортов, причем k из этих изделий – первого сорта, а остальные изделия – второго сорта.

Найти вероятность того, что взятые наугад два изделия окажутся:

а) одного сорта;

б) разных сортов.

n = 70;             k = 45;

Задание 30

Вероятность изготовления изделия с браком на данном предприятии равна 0,04. Перед выпуском изделие подвергается упрощенной проверке, которая в случае

бездефектного изделия пропускает его с вероятностью 0,98, а в случае изделия с дефектом – с вероятностью 0,05.

а) Определить, какая часть изготовленных изделий выходит с предприятия, после упрощенной проверки.

б) Какова вероятность того, что изделие, выдержавшее упрощенную проверку, оказалось дефектным?

Задание 33

Вероятность того, что в результате проверки изделию будет присвоен знак «изделие высшего качества» равна p.

1) На контроль поступило n изделий. Какова вероятность того, что знак высшего качества будет присвоен:

а) ровно m изделиям;

б) более чем k изделиям;

в) хотя бы одному изделию;

г) указать наивероятнейшее количество изделий, получивших знак высшего качества, и найти соответствующую ему вероятность.

2). При тех же условиях найти вероятность того, что в партии из N изделий знак высшего качества получает:

а) ровно половина изделий;

б) не менее чем  k₁, но не более, чем k₂ изделий.

n=6;   p=0,2;   m=3;   k=4;   N=28;   k₁= 4;    k₂=14.

Задание 44

В лотерее на каждые 100 билетов приходится m₁ билетов с выигрышем a₁ тыс. рублей, m₂ билетов с выигрышем a₂ тыс. рублей,  m₃ билетов с выигрышем a₃ тыс. рублей и т.д.

Остальные билеты из сотни не выигрывают.

Составить закон распределения величины выигрыша для владельца одного билета и найти его основные характеристики: математическое ожидание, дисперсию и среднее

квадратическое отклонение. Пояснить смысл указанных характеристик.

а₁=16;     а₂=10;    а₃= 6;    а₄= 3;     а₅= 2;     а₆= 1;

m₁=2;     m₂=5;     m₃=8;   m₄=10;    m₅=15;   m₆=20.

Задание 58

Вес изготовленного серебряного изделия должен составлять а граммов.

При изготовлении возможны случайные погрешности, в результате которых вес изделия случаен, но подчинен нормальному закону распределения со средним квадратическим отклонением σ граммов.

Требуется найти вероятность того, что:

а) вес изделия составит от α до β граммов;

б) величина погрешности в весе не превзойдет δ граммов по абсолютной величине.

a = 130;           σ = 5;              α = 125;          β = 140;          δ = 12;

Задание 64

По итогам выборочных обследований для некоторой категории сотрудников величина их дневного заработка X руб. и соответствующее количество сотрудников n_i

представлены в виде интервального статистического распределения.

а) Построить гистограмму относительных частот распределения.

б) Найти основные характеристики распределения выборочных данных: среднее выборочное значение, выборочную дисперсию и выборочное среднее квадратическое отклонение.

в) Оценить генеральные характеристики по найденным выборочным характеристикам.

г) Считая, что значения признака X в генеральной совокупности подчинены нормальному закону распределения, найти доверительный интервал для оценки математического

ожидания (генерального среднего значения) с надежностью γ , считая, что генеральная дисперсия равна исправленной выборочной дисперсии.

Задание 71

С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев:

X – величина месячной прибыли в тыс. руб., Y – месячные издержки в процентах к объему продаж.

Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые

наблюдались соответствующие пары значений названных признаков.

а) По данным корреляционной таблицы найти  условные средние 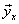 и .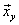

б) Оценить тесноту линейной связи между признаками X и Y.

в) Составить уравнения линейной регрессии Y по X и X по Y .

г) Сделать чертеж, нанеся на него условные средние и найденные прямые регрессии.

д) Оценить силу связи между признаками с помощью корреляционного отношения.