Задание 1. Рабочий
обслуживает три станка. В течение смены первый станок работает бесперебойно в
среднем (90 + (К + М)(mod6))% всего времени,
второй – (80 + (К + М)(mod6))%,
третий – (90 – (К + М)(mod6))%. Найти вероятность того, что среди этих станков
в течение смены:
а) только один будет работать
бесперебойно; b) два будут работать бесперебойно;
с) не менее двух будут работать
бесперебойно; d) хотя бы один будет работать бесперебойно; е) все станки
будут работать либо бесперебойно, либо нет.
Задание 2. В группе
из 25 + (К + М)(mod6) студентов, пришедших сдавать экзамен, имеется 2 + (К +
М)(mod6) подготовленных отлично, 6 + (К + М)(mod6) – хорошо,
12 – (К + М)(mod6) –
удовлетворительно, а остальные студенты подготовлены плохо. Отлично
подготовленные студенты знают все 35 + (К + М)(mod6)
вопросов программы,
подготовленные хорошо – 28 + (К + М)(mod6), подготовленные удовлетворительно –
19 + (К + М)(mod6) и подготовленные плохо знают
лишь 8 + (К + М)(mod6) вопросов
программы из 35 + (К + М)(mod6).
Определить вероятность того, что
вызванный наугад из данной группы студент ответит хотя бы на один из трех
заданных ему вопросов программы.
На экзамене наугад вызванный
студент ответил на один вопрос из трех заданных. Как вероятнее всего он
подготовлен?
Задание 3. В
результате проверки качества приготовленных для посева семян огурца
установлено, что в среднем (85 + (К + М)(mod6))% семян всхожи.
Какова вероятность того, что
среди 200 посеянных семян доля взошедших будет:
а) равна (83 + (К + М)(mod6))%;
b) не менее 83 + (К + М)(mod6))%; с) не более (90 + (К + М)(mod6))%; d) не
менее (82 + (К + М)(mod6))%, но не более (88 + (К + М)(mod6))%?
Сколько нужно посеять семян,
чтобы с вероятностью 0,94 + ((К + М)(mod6))/100 можно было утверждать, что
доля взошедших семян среди них отклонится по абсолютной
величине от вероятности взойти
каждому семени не более, чем на (1 + (К + М)(mod6))/100?
Задание 4. На пути
движения автомобиля четыре светофора, каждый из которых (независимо от других)
запрещает дальнейшее движение автомобиля с вероятностью
0,6 – (К + М)(mod3))/10.
Рассматривается случайная величина с.в. ξ – число светофоров, пройденных
автомобилем без остановки.
Составить ряд распределения с.в. ξ
и представить его графически.
Найти функцию распределения с.в. ξ
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Определить вероятности: а) Р{ξ<Mξ}; b) Р{ξ>Mξ+1};
c) Р{|ξ-Mξ|≤σ(ξ)}
Задание 5. Годовой
облагаемый налогом доход ξ (в тыс. у.е.) наудачу выбранного частного
предпринимателя города N является случайным с плотностью распределения
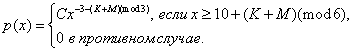
Установить неизвестную постоянную
С и построить график функции p(x).
Найти функцию распределения с.в. ξ
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Во сколько раз число частных
предпринимателей города N с доходом, облагаемым налогом меньше среднего,
превышает число частных предпринимателей с доходом, облагаемым налогом больше
среднего?
Задание 6. При
проверке длины 25 деталей изготовленных станком – автоматом были обнаружены
следующие отклонения от номинала (в мм)*
– 0.307, 0.262, – 0.372,
0.765, – 0.140, – 0.371, – 0.113, – 0.693, – 0.550, – 0.694,
0.545, 0.509, – 0.150, –
0.150, – 0.559, – 0.065, – 0.112, 0.077, 0.698, – 0.119,
0.861, 0.386, – 0.827,
0.908, – 0.047.
Необходимо:
1. Определить исследуемый признак
и его тип (дискретный или непрерывный).
2. В зависимости от типа признака
построить полигон или гистограмму относительных частот.
3. На основе визуального анализа
полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
4. Вычислить выборочные
характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое
(стандартное) отклонение.
5. Используя критерий согласия
«хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в
п.3 закону распределения при уровне значимости 0,05.
6. Для генеральной средней и
дисперсии построить доверительные интервалы, соответствующие доверительной
вероятности 0,95.
7. С надежностью 0,95 проверить
гипотезу о равенстве:
а) генеральной средней значению С;
б) генеральной дисперсии значению
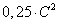 , где С =
1 + (К + М)/100.
, где С =
1 + (К + М)/100.
* Для получения Ваших конкретных
данных все значения выборки следует умножить на число С = 1 + (К + М)/100.



