Задание 1. У сборщика
имеется 10 + (К + М)(mod6) новых и 5 + (К + М)(mod6) бывших в употреблении
(б/у) деталей, которые мало отличаются друг
от друга по внешнему виду.
Сборщик наудачу берет три детали. Найти вероятность того, что среди них будет:
а) только одна деталь б/у; b)
две детали б/у; с) не менее двух деталей б/у;
d) хотя бы одна деталь б/у; е)
все детали одного типа (новые или б/у).
Задание 2. В торговую
фирму поступили телевизоры от трех поставщиков в соотношении 2 : 1 : 2. Практика
показала, что телевизоры, поступающие от первого,
второго и третьего поставщиков,
не требуют ремонта в течение гарантийного срока в среднем соответственно в (80
+ (К + М)(mod6))%,
(90 + (К + М)(mod6))%, (85 + (К
+ М)(mod6))% случаев.
Определить вероятность того, что
из двух поступивших в торговую фирму телевизоров хотя бы один потребует ремонта
в течение гарантийного срока.
Два проданных телевизора не
потребовали ремонта в течение гарантийного срока. От каких поставщиков
вероятнее всего они поступили?
Задание 3. Из-за
болезни на работу ежедневно не выходит в среднем (1 + (К+М)(mod6))% работников
предприятия.
Какова вероятность того, что из 5
+ (К + М)(mod4) работников, выбранных наудачу из списочного состава
предприятия, на работе будет присутствовать:
а) ровно 3 + (К + М)(mod4);
b) не менее 3 + (К + М)(mod4);
с) не более 3 + (К + М)(mod4);
d) хотя бы один сотрудник предприятия?
Вычислить вероятность того, что
на данном предприятии, насчитывающем сто работников, в наудачу выбранный день
из-за болезни будут отсутствовать:
а) 1 + (К + М)(mod6); b) более 1
+ (К + М)(mod6); с) менее 1 + (К + М)(mod6); d) хотя бы один работник
предприятия.
Задание 4. Студент
знает 20 + (К + М)(mod6) вопросов из имеющихся 30 + (К + М)(mod6) вопросов
программы по теории вероятностей и математической статистике.
Экзаменационный билет содержит
четыре произвольных вопроса программы. Студент получает на экзамене отличную
оценку («пять»), если он знает все
вопросы билета; хорошую оценку
(«четыре»), если знает три вопроса; удовлетворительную оценку («три»), если
знает два вопроса; в остальных случаях он получает
неудовлетворительную оценку
(«два»). Рассматривается случайная величина (с.в.) ξ – оценка, которую
студент получит на экзамене.
Составить ряд распределения с.в. ξ
и представить его графически.
Найти функцию распределения с.в. ξ
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Определить вероятности: а) Р{ξ<Mξ}; b) Р{ξ>Mξ+1};
c) Р{|ξ-Mξ|≤σ(ξ)}
Задание 5. Время ξ
(в мин.) ожидания заправки автомашины на АЗС города N является случайным с
плотность распределения
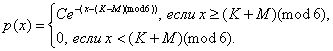
Установить неизвестную
постоянную С и построить график функции p(x).
Найти функцию распределения с.в. ξ
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Во сколько раз число автомашин,
ожидающих заправку меньше среднего времени, превышает число автомашин,
ожидающих заправку больше среднего времени?
Задание 6. Компания,
занимающаяся развитием кабельного телевидения в крупном городе N, провела
выборочное обследование времени ежедневного просмотра
телепередач 25 абонентами кабельной
сети. Получены следующие результаты (в часах)*
3.939, 5.190, 2.835, 3.600,
5.670, 3.203, 5.277, 4.374, 0.891, 2.719, 5.180, 4.634, 4.247, 5.144, 5.421,
3.921, 3.439, 5.766, 6.746, 4.015, 6.246, 5.132, 3.565, 4.101, 6.237
Необходимо:
1. Определить исследуемый признак
и его тип (дискретный или непрерывный).
2. В зависимости от типа признака
построить полигон или гистограмму относительных частот.
3. На основе визуального анализа
полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
4. Вычислить выборочные
характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое
(стандартное) отклонение.
5. Используя критерий согласия
«хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в
п.3 закону распределения при уровне значимости 0,1.
6. Для генеральной средней и
дисперсии построить доверительные интервалы, соответствующие доверительной
вероятности 0,9.
7. С надежностью 0,9 проверить
гипотезу о равенстве:
а) генеральной средней значению
5С;
б) генеральной дисперсии значению
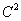 , где С =
1 + (К + М)/100.
, где С =
1 + (К + М)/100.
Для получения Ваших конкретных
данных все значения выборки следует умножить на число С = 1 + (К + М)/100.



