Задание 1. Экспедиция
издательства отправляет газеты в три почтовых отделения. Известно, что в первое
отделение газеты доставляются своевременно в среднем
в (92 + (К + М)(mod6))% всех
случаев, во второе – (85 + (К + М)(mod6))%, в третье – (95 – (К + М)(mod6))%.
Найти вероятность того, что из трех почтовых отделений:
а) только одно получит газеты
вовремя; b) два получат газеты вовремя;
с) не менее двух получат газеты
вовремя; d) хотя бы одно получит газеты вовремя; е) все отделения либо
получат газеты вовремя, либо нет.
Задание 2. В ящике 15
+ (К + М)(mod6) теннисных мячей, из которых 10 + (К + М)(mod6) новых. Для
первой игры наудачу берут три мяча, которые после игры
возвращают в ящик. Для второй
игры также наудачу берут из ящика три мяча.
Определить вероятность того, что
все три мяча, взятые для второй игры, будут новыми.
Из взятых для второй игры трех
мячей один оказался не новым. Сколько новых мячей вероятнее всего было взято
для первой игры?
Задание 3. По
результатам проверок налоговыми инспекциями установлено, что в среднем каждое 4
+ (К + М)(mod4)-е малое предприятие города N нарушает финансовую дисциплину.
Какова вероятность того, что из
ста малых предприятий города N нарушения финансовой дисциплины будут иметь:
а) 5 · (5 – (К + М)(mod4)); b)
не менее 4 · (5 – (К + М)(mod4));
с) не более 6 · (5 – (К +
М)(mod4)); d) не менее 4 · (5 – (К + М)(mod4)), но не более 6 · (5 – (К +
М)(mod4)) предприятий.
Задание 4. Охотник,
имеющий четыре патрона, стреляет по цели до тех пор, пока не попадет или не израсходует
все патроны. Известно, что в цель данного вида он
попадает в среднем 5 + (К +
М)(mod4) раз из десяти выстрелов. Рассматривается случайная величина (с.в.) ξ
– число израсходованных охотником патронов.
Составить ряд распределения с.в. ξ
и представить его графически.
Найти функцию распределения с.в. ξ
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Определить вероятности: а) Р{ξ<Mξ}; b) Р{ξ>Mξ+1};
c) Р{|ξ-Mξ|≤σ(ξ)}
Задание 5. При
исследовании некоторого непрерывного признака ξ экспериментатор
предположил, что этот признак подчиняется закону распределения с плотностью
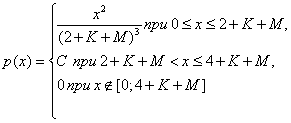
При каком значении С
экспериментатор будет прав? Построить график плотности распределения.
Найти функцию распределения с.в. ξ
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Во сколько раз число опытов, в
которых экспериментатор будет получать результат меньше среднего значения,
превышает число опытов, в которых результат будет больше среднего значения?
Задание 6. Выборка из
большой партии микросхем нового типа содержит 25 микросхем. Время непрерывной работы
до выхода из строя для этих микросхем оказалось равным (в сутках)*
37.48, 36.72, 36.75, 37.64,
35.41, 36.28, 36.36, 36.96, 37.29, 36.53, 36.55, 35.75, 36.47, 35.91, 34.90,
34.45, 34.40, 35.86, 37.30, 36.08, 35.63, 35.02, 35.19, 36.16, 33.93
Необходимо:
1. Определить исследуемый признак
и его тип (дискретный или непрерывный).
2. В зависимости от типа признака
построить полигон или гистограмму относительных частот.
3. На основе визуального анализа
полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
4. Вычислить выборочные
характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое
(стандартное) отклонение.
5. Используя критерий согласия
«хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в
п.3 закону распределения при уровне значимости 0,01.
6. Для генеральной средней и
дисперсии построить доверительные интервалы, соответствующие доверительной
вероятности 0,99.
7. С надежностью 0,99 проверить
гипотезу о равенстве:
а) генеральной средней значению
36С;
б) генеральной дисперсии значению
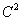 , где С
= 1 + (К + М)/100.
, где С
= 1 + (К + М)/100.
* Для получения Ваших конкретных
данных все значения выборки следует умножить на число С = 1 + (К + М)/100.



