Задание 1. Студент
знает 15 + (К + М)(mod6) вопросов программы по теории вероятностей и
математической статистике из 25 + (К + М)(mod6).
На зачете ему предлагается три
наудачу выбранных из программы вопроса. Найти вероятность того, что студент
ответит:
а) только на один вопрос; b) на
два вопроса; с) не менее, чем на два вопроса;
d) хотя бы на один вопрос; е)
либо на все вопросы, либо ни на один.
Задание 2. На складе
находятся одинаковые изделия, изготовленные тремя заводами: первым заводом
произведено (30 + (К + М)(mod6))% всех изделий,
вторым – (35 + (К + М)(mod6))%, а
остальные изделия с третьего завода. Известно, что из каждой сотни изделий
удовлетворяют стандарту в
среднем 90 + (К + М)(mod6)
изделий, изготовленных на первом заводе, 95 – (К + М)(mod6) – на втором, 85 +
(К + М)(mod6) – на третьем.
Для контроля качества со склада
наудачу берут два изделия.
1. Определить вероятность того,
что по крайней мере одно из проверяемых изделий будет нестандартным.
2. Оба проверяемых изделия
оказались стандартными. На каких заводах вероятнее всего они изготовлены?
Задание 3. При
опускании одной монеты автомат срабатывает неправильно в среднем в 1 + (К +
М)(mod6) случаях из ста.
1. Какова вероятность того, что
при опускании 5 + (К + М)(mod4) монет автомат сработает правильно:
а) 3 + (К + М)(mod4); b) не
менее 3 + (К + М)(mod4);
с) не более 3 + (К + М)(mod4);
d) хотя бы один раз?
2. В течение суток в автомат было
опущено сто монет. Вычислить вероятность того, что автомат при этом сработал
неправильно:
а) 1 + (К + М)(mod6); b) более
1 + (К + М)(mod6);
с) менее 1 + (К + М)(mod6); d)
хотя бы один раз.
Задание 4. Произведено
три независимых выстрела по удаляющейся цели. Вероятность попадания при i-том
выстреле равна 1 – ((К + М)(mod4) + i)/10, i = 1, 2, 3.
Рассматривается случайная
величина (с.в.) ξ – число попаданий в цель.
Составить ряд распределения с.в.
ξ и представить его графически.
Найти функцию распределения с.в.
ξ и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Определить вероятности: а) Р{ξ<Mξ}; b) Р{ξ>Mξ+1};
c) Р{|ξ-Mξ|≤σ(ξ)}
Задание 5. Обработка
результатов переписи населения в городе N показала, что плотность
распределения возраста ξ (в годах) лиц, занимающихся малым
бизнесом, может быть представлена
функцией
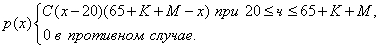
Установить неизвестную
постоянную С и построить график функции p(x).
Найти функцию распределения с.в.
ξ и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Во сколько раз число бизнесменов
в возрасте ниже среднего превышает число бизнесменов в возрасте выше среднего?
Задание 6. Для
определения нормы времени на выполнение определенной технологической операции
на конвейере часов проведено 25 экспериментов.
Получены следующие результаты (в
часах)*
0.828, 0.542, 0.890, 0.705,
0.491, 1.384, 0.379, 0.242, 0.866, 0.321, 0.627, 1.012, 0.579, 0.477, 0.490,
1.079, 0.443, 0.374, 0.937, 0.529, 0.912, 0.949, 0.906, 0.794, 0.735.
Необходимо:
1. Определить исследуемый признак
и его тип (дискретный или непрерывный).
2. В зависимости от типа признака
построить полигон или гистограмму относительных частот.
3. На основе визуального анализа
полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
4. Вычислить выборочные
характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое
(стандартное) отклонение.
5. Используя критерий согласия
«хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в
п.3 закону распределения при уровне значимости 0,05.
6. Для генеральной средней и
дисперсии построить доверительные интервалы, соответствующие доверительной
вероятности 0,95.
7. С надежностью 0,95 проверить
гипотезу о равенстве:
а) генеральной средней значению
0,75×С;
б) генеральной дисперсии значению
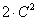 , где C
= 1 + (K + M)/100.
, где C
= 1 + (K + M)/100.
* Для получения Ваших конкретных
данных все значения выборки следует умножить на число C = 1 + (K + M)/100.



