Задание 1. На стройку
от трех разных поставщиков должны поступить три партии материалов. Известно,
что первый поставщик доставляет материалы своевременно
в среднем в (90 + (К + М)(mod6))%
всех случаев, второй – в (80 + (К + М)(mod6))%, третий – в (95 – (К +
М)(mod6))%. Найти вероятность того, что из трех партий на
стройку будет доставлена
своевременно:
а) только одна; b) две; с) не
менее двух;
d) хотя бы одна; е) либо все
партии, либо ни одна.
Задание 2. Имеется
коробка с 3 + (К + М)(mod4) изделиями одного образца, причем среди них с
одинаковой вероятностью возможно любое количество
бракованных изделий (от 0 до 3 +
(К + М)(mod4)). Из коробки наудачу выбирается одновременно три изделия.
Определить вероятность того, что
среди извлеченных изделий будет хотя бы одно бракованное.
Извлеченные из коробки три
изделия оказались одного типа (бракованные или небракованные). Какой состав
коробки с изделиями вероятнее всего?
Задание 3. При
социологических опросах граждан города N установлено, что в среднем (10 + (К +
М)(mod6))% дают неискренний ответ.
Какова вероятность того, что при
опросе 500 граждан города N доля неискренних ответов будет:
а) равна (8 + (К + М)(mod6))%;
b) не менее (8 + (К + М)(mod6))%;
с) не более (15 + (К +
М)(mod6))%; d) не менее (7 + (К + М)(mod6))%, но не более (13 + (К +
М)(mod6))%?
Сколько нужно опросить граждан
города N, чтобы с вероятностью 0,94 + ((К + М)(mod6))/100 можно было
утверждать, что доля неискренних ответов среди них
отклонится по абсолютной величине
от вероятности получения неискреннего ответа от каждого опрашиваемого не более,
чем на (1 + ((К + М)(mod6))/100?
Задание 4. Из
поступивших в ремонт 10 + (К + М)(mod6) часов 6 + (К + М)(mod6) нуждаются в
общей чистке механизма. Часы не рассортированы по виду
ремонта. Мастер, желая найти
часы, нуждающиеся в чистке, рассматривает их поочередно и, найдя такие часы,
прекращает дальнейший просмотр.
Рассматривается случайная
величина (с.в.) ξ – число просмотренных часов.
Составить ряд распределения с.в. ξ
и представить его графически.
Найти функцию распределения с.в. ξ
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Определить вероятности: а) Р{ξ<Mξ}; b) Р{ξ>Mξ+1};
c) Р{|ξ-Mξ|≤σ(ξ)}
Задание 5. При
исследовании некоторого непрерывного признака ξ экспериментатор
предположил, что этот признак подчиняется закону распределения с плотностью
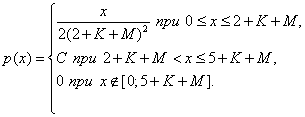
При каком значении С
экспериментатор будет прав? Построить график плотности распределения.
Найти функцию распределения с.в. ξ
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Во сколько раз число опытов, в
которых экспериментатор будет получать результат больше среднего значения,
превышает число опытов, в которых результат будет меньше среднего значения?
Задание 6. Служба
контроля Энергосбыта провела проверку расхода электроэнергии в течение месяца
25 квартиросъемщиками однокомнатных квартир города N. Получены следующие
результаты (в кВт. ч.)*
155.1, 167.2, 175.9, 166.1,
170.0, 183.1, 178.3, 181.1, 157.7, 158.4, 158.4, 168.9, 155.3, 132.4, 194.1,
186.9, 177.1, 159.9, 161.1, 161.8, 179.2, 169.0, 194.5, 154.3, 180.7.
Необходимо:
1. Определить исследуемый признак
и его тип (дискретный или непрерывный).
2. В зависимости от типа признака
построить полигон или гистограмму относительных частот.
3. На основе визуального анализа
полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
4. Вычислить выборочные
характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое
(стандартное) отклонение.
5. Используя критерий согласия
«хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в
п.3 закону распределения при уровне значимости 0,05.
6. Для генеральной средней и
дисперсии построить доверительные интервалы, соответствующие доверительной
вероятности 0,95.
7. С надежностью 0,95 проверить
гипотезу о равенстве:
а) генеральной средней значению
150×С;
б) генеральной дисперсии значению
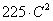 , где C
= 1 + (K + M)/100.
, где C
= 1 + (K + M)/100.
* Для получения Ваших конкретных
данных все значения выборки следует умножить на число C = 1 + (K + M)/100.



