Задание 1. Охотник
стреляет три раза по удаляющейся цели. Вероятность попадания в цель в начале
стрельбы равна 0,9 – ((К + М)(mod6))/100, а
после каждого выстрела
уменьшается на 0,1. Найти вероятность того, что охотник попадет:
а) только один раз; b) два
раза; с) не менее двух раз;
d) хотя бы один раз; е) все три
раза или все три раза промахнется.
Задание 2. Магазин
торгует телевизорами двух марок А и В, пользующихся одинаковым спросом
населения. За день торговли из
имеющихся 4 + (К + М)(mod4) телевизоров
марки А и (6 + (К + М)(mod4)) телевизоров марки В было продано два
телевизора.
На следующий день магазин
получил 6 – (К + М)(mod4) телевизоров А и 4 – (К + М)(mod4) телевизора
марки В. За второй день торговли продали три телевизора.
Определить вероятность того, что
по крайней мере один из проданных во второй день телевизоров – марки А.
Проданные во второй день –
телевизоры марки А. Телевизоры каких марок вероятнее всего были проданы в
первый день торговли?
Задание 3. В среднем
(20 + (К + М)(mod6))% пакетов акций на аукционе продаются по первоначально
заявленной цене.
Какова вероятность того, что из
5 + (К + М)(mod4) наугад взятых пакетов акций будет продано по другой (не
первоначально заявленной) цене:
а) ровно 3 + (К + М)(mod4); b)
более 3 + (К + М)(mod4);
с) менее 3 + (К + М)(mod4); d)
хотя бы один пакет акций?
Вычислить вероятность того, что
из ста выставленных на аукционе пакетов акций по первоначально заявленной цене
будет продано:
а) 18 + (К + М)(mod6); b) не
менее (18 + (К + М)(mod6));
с) не более 23 + (К + М)(mod6);
d) не менее 15 + (К + М)(mod6), но не более
25 + (К + М)(mod6) пакетов
акций.
Задание 4. В партии
из 10 + (К + М)(mod6) изделий содержится 3 + (К + М)(mod6) бракованных. Для
проверки качества изделий контролер из всей партии
наугад выбирает одновременно три
изделия. Рассматривается случайная величина (с.в.) ξ – число бракованных
изделий, содержащихся в выборке.
Составить ряд распределения с.в.
ξ и представить его графически.
Найти функцию распределения с.в.
ξ и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Определить вероятности: а) Р{ξ<Mξ}; b) Р{ξ>Mξ+1};
c) Р{|ξ-Mξ|≤σ(ξ)}
Задание 5. Время ξ
(в мин.) между прибытием двух автомашин к светофору является случайным с
плотностью распределения
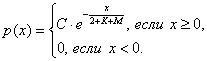
Установить неизвестную
постоянную С и построить график функции p(x).
Найти функцию распределения с.в.
ξ и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Во сколько раз число прибывших к
светофору автомашин со временами между прибытиями больше среднего превосходит
число автомашин со временами между прибытиями меньше среднего?
Задание 6. При
измерении веса 25 упаковок сильнодействующего лекарственного препарата были
обнаружены следующие отклонения (в гр.) от указанного на обертке*
–24.34, –14.59, –18.27,
–8.94, –15.09, –10.94, 4.47, 3.05, –8.33, –22.98, 1.75,
–32.07, –7.43, –18.63,
–12.97, –11.08, –7.44, –1.70, 6.34, –11.08, –11.12, –15.90,
–10.26, –8.07, –6.48.
Необходимо:
1. Определить исследуемый признак
и его тип (дискретный или непрерывный).
2. В зависимости от типа признака
построить полигон или гистограмму относительных частот.
3. На основе визуального анализа
полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
4. Вычислить выборочные
характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое
(стандартное) отклонение.
5. Используя критерий согласия
«хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в
п.3 закону распределения при уровне значимости 0,05.
6. Для генеральной средней и
дисперсии построить доверительные интервалы, соответствующие доверительной
вероятности 0,95.
7. С надежностью 0,95 проверить
гипотезу о равенстве:
а) генеральной средней значению
–10×С;
б) генеральной дисперсии значению
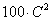 , где C
= 1 + (K + M)/100.
, где C
= 1 + (K + M)/100.
* Для получения Ваших конкретных
данных все значения выборки следует умножить на число C = 1 + (K + M)/100.



