Задание 1. Вероятность
того, что студент сдаст в сессию первый экзамен равна 0,9 + ((К +
М)(mod6))/100, второй – 0,8 + ((К + М)(mod6))/100,
третий – 0,9 – ((К +
М)(mod6))/100. Найти вероятность того, что данный студент:
а) сдаст только один экзамен; b)
сдаст два экзамена;
с) сдаст не менее двух
экзаменов; d) сдаст хотя бы один экзамен;
е) все экзамены либо сдаст, либо
завалит.
Задание 2. Имеются две
партии, содержащие 10 + (К + М)(mod6) и 15 + (К + М)(mod6) одинаковых
изделий. В первой партии 3 + (К + М)(mod6),
во второй – 6 + (К + М)(mod6)
бракованных изделий, а остальные изделия стандартные. Из первой партии во
вторую наудачу перекладывают два изделия,
после чего из второй партии также
наудачу одновременно берут два изделия.
Определить вероятность того, что
по крайней мере одно изделие, взятое из второй партии, окажется стандартным.
Из двух изделий, взятых из второй
партии, одно оказалось бракованным, а другое – стандартным. Какие изделия
вероятнее всего переложили из первой партии во вторую?
Задание 3. В некотором
автопарке ежедневно в среднем (94 + (К + М)(mod6))% автомобилей исправны.
Какова вероятность того, что
среди 5 + (К + М)(mod4) наудачу выбранных автомобилей неисправных будет:
а) ровно 3 + (К + М)(mod4);
b) не менее 3 + (К + М)(mod4);
с) не более 3 + (К + М)(mod4);
d) хотя бы один автомобиль?
Вычислить вероятность того, что в
данном автопарке, имеющем сто автомобилей, в наудачу выбранный день неисправным
будет:
а) 6 – (К + М)(mod6);
b) более 6 – (К + М)(mod6);
с) менее 6 – (К + М)(mod6); d)
хотя бы один автомобиль.
Задание 4. В рекламных
целях торговая фирма вкладывает в каждую 6 + (К + М)(mod5)-ю единицу товара
денежный приз размером 100 руб. Рассматривается случайная
величина (с.в.) x – размер выигрыша при четырех покупках
продукции данной фирмы.
Составить ряд распределения с.в. ξ
и представить его графически.
Найти функцию распределения с.в. ξ
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое (стандартное)
отклонение σ(ξ).
Определить вероятности: а) Р{ξ<Mξ}; b) Р{ξ>Mξ+1};
c) Р{|ξ-Mξ|≤σ(ξ)}
Задание 5. Время ξ
(в годах) безотказной работы электроннолучевой трубки телевизора является
случайным с плотностью распределения
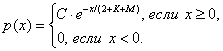
Установить неизвестную
постоянную С и построить график функции p(x).
Найти функцию распределения с.в. ξ
и построить её график.
Вычислить математическое ожидание
(среднее значение) Мξ, дисперсию Dξ и среднее квадратическое
(стандартное) отклонение σ(ξ).
Во сколько раз число
электроннолучевых трубок со временем безотказной работы больше среднего
превышает число трубок со временем безотказной работы меньше среднего?
Задание 6. Исследуется
диаметр горошин перед контрольными посевами. Выборочное обследование 25 горошин
дало следующие результаты (в мм)*
8.182, 7.515, 8.326,
7.894, 7.396, 9.480, 7.135, 6.814, 8.271, 7.000,
7.712, 8.612, 7.602,
7.363, 7.393, 8.768, 7.284, 7.124, 8.437, 7.484,
8.379, 8.465, 8.364,
8.102, 7.964.
Необходимо:
1. Определить исследуемый признак
и его тип (дискретный или непрерывный).
2. В зависимости от типа признака
построить полигон или гистограмму относительных частот.
3. На основе визуального анализа
полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
4. Вычислить выборочные
характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое
(стандартное) отклонение.
5. Используя критерий согласия
«хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в
п.3 закону распределения при уровне значимости 0,1.
6. Для генеральной средней и
дисперсии построить доверительные интервалы, соответствующие доверительной
вероятности 0,9.
7. С надежностью 0,9 проверить
гипотезу о равенстве:
а) генеральной средней значению
8×С;
б) генеральной дисперсии значению
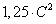 , где C
= 1 + (K + M)/100.
, где C
= 1 + (K + M)/100.
* Для получения Ваших конкретных
данных все значения выборки следует умножить на число C = 1 + (K + M)/100.



